UV VIS Spektroskopie

UV/VIS-Spektroskopie an zweiatomigen Molekülen

 

Versuchsbetreuer: Tim Lämmerzahl  
Phone: 33060

Mail to Tim

 

Zielsetzung

In diesem Versuch sollen die Eigenschaften der Bindung des I2 Moleküls untersucht werden. Hierzu wird ein UV/Vis-Spektrum aufgenommen, dessen Daten anhand des Modells des anharmonischen Oszillators ausgewertet werden. Wir orientieren uns dabei stark an der Abhandlung von Mac Naught.

Einführung

Wird ein Molekül mit UV- oder sichtbarem Licht bestrahlt, so kann es  durch Absorption eines Photons Energie zur Elektronenanregung  aufnehmen, wobei ein Elektron von einem energetisch nieder gelegenes  Orbital in ein energetisch höher 
gelegenes Orbital übergeht. Bei Raumtemperatur befinden sich die meisten  Moleküe im niedrigsten elektronischen Zustand, dem elektronischen Grundzustand. Man spricht in diesem Fall auch von einem Übergang vom Grundzustand in einen angeregten Zustand.

Die elektronische Anregung kann zusätzlich von Schwingungs- und  Rotationsanregungen begleitet werden. Die Energieänderung des Moleküls setzt sich dann zusammen aus einem elektronischen, einem 
vibronischen und einem rotatorischen Anteil:
$$
\Delta E_{\mathrm{ges}} = \Delta E_{\mathrm{el}} + \Delta E_{\mathrm{vib}} + \Delta E_{\mathrm{rot}}. 
\label{c1gl1}
$$

Nach der Absorption kann das Molekül durch die Emission von 
Licht wieder von dem angeregten Zustand in den Grundzustand übergehen. 
Auch hier können gleichzeitig Rotations- und  Schwingungsübergänge erfolgen. Es gilt das Franck-Condon-Prinzip.

 

Aufgrund der starken Wechselwirkung zwischen den Molekülen in  flüssigen Proben erscheinen die elektronischen Übergänge hier oft nur als breite Absorptionsbanden ohne Schwingungs- und 
Rotationsstruktur. Auch in der Gasphase lässt sich die  Rotationsstruktur nicht immer auflösen, so dass man nur Elektronen-Schwingungs-Spektren  erhält. Im Folgenden wird daher  der rotatorische Anteil $$\Delta E_\mathrm{rot}$$ an der Energieänderung des Moleküls 
vernachlässigt:

$$\Delta E_{\mathrm{ges}} = \Delta E_{\mathrm{el}} + \Delta E_{\mathrm{vib}} . $$

 

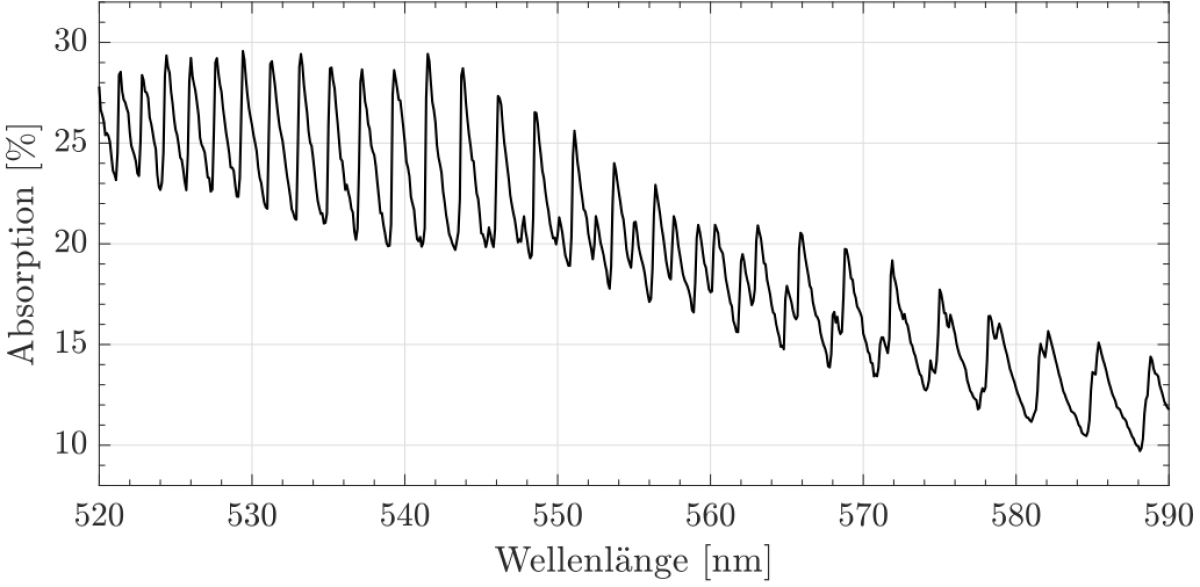
Aus der Schwingungsstruktur eines wie in der  obigen Abbildung  gezeigten Elektronen-Schwingungs-Spektrums lassen sich die Abstände der Schwingungsniveaus desjenigen elektronischen 
Zustandes bestimmen, in den der Übergang erfolgt. Dies soll hier für den Fall eines zweiatomigen Moleküls anhand der Anregung vom Grundzustand in den ersten angeregten Zustand erläutert werden. 
Angenommen wird zunächst, dass sich das Molekül vor der Anregung im 
Schwingungsgrundzustand des elektronischen Grundzustandes befindet, der als $$v_{0}^{''}$$
bezeichnet wird.

Allgemein werden in der Spektroskopie einfach gestrichene 
Quantenzahlen für den energetisch höherliegenden Zustand eines Übergangs verwendet, doppelt gestrichene für den tieferliegenden 
Zustand.

 

Betrachtet man dann die Übergänge in zwei benachbarte 
Schwingungsniveaus des elektronisch angeregten Zustands $$v_{i}'$$
und $$v_{i+1}' , $$ so folgt für diese aus der obigen Gleichung :

$$
\Delta E_{i} = E_{v_{i}'} - E_{v_{0}''} 
\label{c1gl4}
$$


und
$$
\Delta E_{i+1} = E_{v_{i+1}'} - E_{v_{0}''} \;.
\label{c1gl5}
$$

 

 

Im Elektronen-Schwingungs-Spektrum erscheinen diese beiden Übergänge
als benachbarte Absorptionsbanden. Für die Energiedifferenz
 
$$ 
\Delta \Delta E_{i,i+1}
$$ zwischen den beiden Übergängen erhält man:
 
 
$$
\Delta E_{i,i+1} = \Delta E_{i+1} - \Delta E_{i} = E_{v_{i+1}'} - E_{v_{i}'} \; .
\label{c1gl6}
$$
 
Analog ergibt sich für den Fall von Übergängen aus benachbarten
Schwingungsniveaus im elektronischen Grundzustand in ein gemeinsames
Schwingungsniveau des elektronisch angeregten Zustandes:
$$
\Delta E_{i,i+1} = \Delta E_{i+1} - \Delta E_{i} = E_{v_{i+1}''} - E_{v_{i}''} \;.
\label{c1gl7}
$$
 
 
Deshalb können wir im Weiteren die Kennzeichnung mit $$'$$ und $$''$$ weglassen.
 
 
Betrachtet man das Molekül als einen anharmonischen Oszillator unter Verwendung des Morse-Potentials, so ergeben sich die Energien $ E_{v_{i}} $ und $ E_{v_{i+1}} $ aus der Lösung der Schrödingergleichung:
 
 
$$
E_{v}=\hbar \omega_\mathrm{e}\cdot \left(v+\frac{1}{2}\right) - \hbar \omega_\mathrm{e}\cdot \chi_\mathrm{e} \cdot \left(v+\frac{1}{2}\right)^{2} \; {\rm mit}\; \; v = 0,1,2 \cdots v_\mathrm{max}
\label{c1gl8}
$$
 
 
 
In dieser Gleichung entspricht $$ \chi_\mathrm{e}$$ einer Anharmonizitätskonstanten
und $$\omega_\mathrm{e}$$ einer Schwingungsfrequenz, die für $$\chi_\mathrm{e}$$ = 0 der Schwingungsfrequenz des harmonischen Oszillators entspricht. Die Schwingungsfrequenz ist dabei mit der Kraftkonstanten $$k$$ und der reduzierten Masse $$\mu$$ des Moleküls über
 
 
 
$$
\omega_\mathrm{e}= \sqrt{\frac{k}{\mu}}
\label{c1gl9}
$$
 
 
 
verknüpft. Es  ergibt sich für die Energiedifferenz $$\Delta E_{i,i+1}$$:
 
$$
\Delta \Delta E_{i,i+1} = \hbar \omega_\mathrm{e} -2 \hbar \omega_\mathrm{e}\chi_\mathrm{e} - 2 \hbar \omega_\mathrm{e}\chi_\mathrm{e}v_{i}
\label{c1gl10}
$$
 
 
 
Mit den bekannten Gleichungen $ \Delta E = h \nu $, $c= \lambda \nu $, $\omega_{e} = 2 \pi \nu_\mathrm{e}$, und
$\tilde{\nu} = 1/\lambda$ lässt sich dies schlie{\ss}lich zu
\begin{equation}
\Delta \tilde{\nu}_{i,i+1} = \tilde{\nu}_\mathrm{e} -2 \tilde{\nu}_\mathrm{e}\chi_\mathrm{e} - 2 \tilde{\nu}_\mathrm{e}\chi_\mathrm{e} \cdot v_{i}
\label{c1gl11}
\end{equation}
umformen. Dabei entspricht $ \Delta \tilde{\nu}_{i,i+1}$ der Differenz zwischen den Wellenzahlen der entsprechenden Absorptionsbanden im Elektronen-Schwingungs-Spektrum. Lassen sich die Absorptionsbanden im Spektrum den einzelnen Schwingungsniveaus $v_{i}$ zuordnen, so kann eine \textbf{Birge-Sponer-Auftragung} angefertigt werden, in dem $ \Delta \tilde{\nu}_{i,i+1}$ gegenüber $v_{i} + 1/2$ aufgetragen wird. Aus der Steigung ergibt sich dann $ 2 \tilde{\nu}_\mathrm{e}\chi_\mathrm{e} $ und aus dem $y$-Achsenabschnitt $ \tilde{\nu}_\mathrm{e} -2 \tilde{\nu}_\mathrm{e}\chi_\mathrm{e}$, so dass die An\-harmonizitäts\-konstante $\chi_\mathrm{e}$ und das Vibrationsquant $\tilde{\nu}_\mathrm{e}$ bestimmt werden können. Desweiteren entspricht der $x$-Achsenabschnitt der Dissoziationsgrenze $v_\mathrm{max}$, oberhalb der das Molekül dissoziiert. Die Fläche unter der Geraden von $v_{0}$ bis $v_\mathrm{max}$ enstspricht der Summe der Energieabstände vom Schwingungsgrundzustand bis zur Dissoziationsgrenze des jeweiligen elektronischen Zustands, wodurch sich die Dissoziationsenergie $D_0$ berechnen lässt.
 
Nach der \textbf{Born-Oppenheimer-Näherung} erfolgt der elektronische
Übergang dabei so schnell, dass die Atomkerne in dieser Zeit ihre
Position nicht ändern, d. h. die Molekülstruktur wird zunächst
beibehalten. Das hat zur Folge, da{\ss} nach einem elektronischen
Übergang die Kerne plötzlich ein neues Kraftfeld spüren. Nach
der klassischen Vorstellung beginnen die Kerne aufgrund dieses neuen
Kraftfeldes dann zu schwingen.
 
Während der Aufnahme eines \textbf{UV/Vis-Spektrums} wird die
Wellenlänge des eingestrahlten Lichtes kontinuierlich bzw. schrittweise geändert. Im
Spektrum erscheinen die vibronischen Übergänge als
Absorptionsbanden bei charakteristischen Wellenlängen.
 
Die Intensität der Absorptionsbande, d. h. $I_{0} - I$, ist proportional zum
Produkt aus der Übergangswahrscheinlichkeit $P$ und der Besetzungszahl $N$ des Ausgangszu\-stands. Nach dem \textbf{Franck-Condon-Prinzip} werden dabei
Übergänge zwischen solchen Schwingunszuständen bevorzugt, bei
denen sich Ort und Impuls der Atomkerne nicht oder nur wenig ändern
m\"ussen.
 
Die Besetzung der Zust\"ande bei einer bestimmten Temperatur $T$ ergibt sich aus der \textbf{Boltzmann-Verteilung}. F\"ur ein System mit zwei Energieniveaus gilt:
\begin{equation}
\frac{N_{2}}{N_{1}}=\exp{\left( -\frac{\Delta E}{k_\mathrm{B} T} \right) }
\label{boltzmanngleichung}
\end{equation}
Hier entsprechen $N_{1}$ und $N_{2}$ den Besetzungen des energetisch tiefer bzw. höher gelegenen Zustands, $k_\mathrm{B}$ der Boltzmannkonstante und $ \Delta E$ der Energiedifferenz zwischen den beiden Niveaus.
 
Die Übergangswahrscheinlichkeit $P$ ist darüber hinaus proportional zum Quadrat des \textbf{Über\-lappungs\-inte\-grals } $S$ der Wellenfunktionen der beteiligten Schwingungszustände $\psi_{m}$ und $ \psi_{n}$, welches auch \textbf{Franck-Condon-Faktor} genannt wird:
\begin{equation}
\frac{I_{n,m}}{N_n} \propto P_{n,m} \propto S_{n,m}^2=\left[\int \psi_{m}^{\ast} \psi_{n} \mathrm{d}r \right]^2 = \braket{\psi_{m}|\psi_{n}}^2 \;.
\end{equation}
 
\begin{figure}[!hb]
\begin{center}
\includegraphics[width=0.7\textwidth]{figures/C1_PotentialCurvesIodine.pdf}
\end{center}
\caption{Im Rahmen des Praktikumsversuchs berechnete Potentialkurven von Iod für den Grundzustand X und den angeregten Zustand B.}
\label{fig:potential_energy_curves}
\end{figure}