Teilprojekt P5
Projektbeschreibung

Adaptiv geglättete molekularstatische Methoden zur Simulation von Ferroelektrika
Ferroelektrika werden auf verschiedenen Längenskalen, von der Elektronenstrukur bis zur Kontinuumsbeschreibung, modelliert und simuliert. Dabei wurden in den vergangen zehn Jahren insbesondere Modelle und Algorithmen auf atomistischer Ebene weiterentwickelt. Dennoch bleibt für akkurate Ergebnisse der Rechenaufwand der etablierten Verfahren erheblich, weshalb auf dem Gebiet der atomistischen Simulationen auch weiterhin neue Methoden entwickelt werden.
Das übergeordnete Ziel dieses Teilprojekts ist die Entwicklung und Untersuchung von adaptiv geglätteten molekularstatischen Methoden zur Mehrskalenanalyse von elektromechanischen Phänomenen in ferroelektrischen Funktionsmaterialien. Dazu muss einerseits eine genaue Abbildung des Materials auf atomarer Ebene erfolgen um relevante Lösungsgebiete, wie beispielsweise Domänenwände, detailliert untersuchen zu können. Andererseits müssen ferroelektrische Strukturen mit technologisch relevanten Längenabmessungen unter mechanischer und elektrischer Belastung, basierend auf atomistischen Berechnungen, simulierbar sein.
Um ferroelektrische Materialien auf der Mikroebene zu simulieren werden bereits seit über einer Dekade sowohl ab initio Simulationen als auch die Molekulardynamik erfolgreich eingesetzt. Dabei bilden nicht nur die geringen Längenskalen sondern insbesondere die Zeitschrittlängen dieser Verfahren einen limitierenden Faktor. Durch den Einsatz molekularstatischer Methoden soll daher die dynamische Problemstellung in ein quasi-statisches Verfahren überführt werden. Des Weiteren wird im Zuge der Mehrskalenanalyse auf das bereits etablierte Verfahren der Quasi-Kontinuums-Methode zurückgegriffen, welches ein Hybridverfahren aus Molekularstatik und der Finite Elemente Methode darstellt.
Neben dem anvisierten methodischen Zugewinn sollen die gewonnen Erkenntnisse direkt in anderen Projekte, die sich mit nicht-atomistischen/phänomenologischen Modellierung von Ferroelektrika beschäftigen, einfließen.
Dielektrische Hysteresekurve von Bariumtitanat
Veröffentlichungen
| Endres, F. & Steinmann, P. (2014), "Molecular statics simulations of head to head and tail to tail nanodomains of rhombohedral barium titanate", Computational Materials Science. Vol. 97, pp. 20-25. |
BibTeX:
@article{Endres2014,
author = {Endres, F. and Steinmann, P.},
title = {Molecular statics simulations of head to head and tail to tail nanodomains of rhombohedral barium titanate},
journal = {Computational Materials Science},
year = {2014},
volume = {97},
pages = {20--25},
note = {P5 DOI: 10.1016/j.commatsci.2014.10.001}
}
|
| Endres, F. & Steinmann, P. (2014), "Molecular static simulations of ferroelectric material hysteresis behaviour", Proceedings in Applied Mathematics and Mechanics. Vol. 14, pp. 409-410. |
BibTeX:
@article{Endres2014a,
author = {Endres, F. and Steinmann, P.},
title = {Molecular static simulations of ferroelectric material hysteresis behaviour},
journal = {Proceedings in Applied Mathematics and Mechanics},
year = {2014},
volume = {14},
pages = {409--410},
note = {P5}
}
|
| Endres, F. & Steinmann, P. (2013), "On molecular statics simulation of ferroelectric barium titanate", Proceedings in Applied Mathematics and Mechanics. Vol. 13, pp. 313-314. |
BibTeX:
@article{Endres2014c,
author = {Endres, F. and Steinmann, P.},
title = {On molecular statics simulation of ferroelectric barium titanate},
journal = {Proceedings in Applied Mathematics and Mechanics},
year = {2013},
volume = {13},
pages = {313--314},
note = {P5}
}
|
| Endres, F. & Steinmann, P. (2014), "An extended molecular statics algorithm simulating the electromechanical continuum response of ferroelectric materials", Computational Mechanics. Vol. 51, pp. 2144-2156. |
BibTeX:
@article{EndSte:CM,
author = {Endres, F. and Steinmann, P.},
title = {An extended molecular statics algorithm simulating the electromechanical continuum response of ferroelectric materials},
journal = {Computational Mechanics},
year = {2014},
volume = {51},
pages = {2144--2156},
note = {DOI: 10.1007/s00466-014-1072-7 P5}
}
|
| Keip, M.-A., Steinmann, P. & Schröder, J. (2014), "Two-scale computational homogenization of electroelasticity at finite strains", Computer Methods in Applied Mechanics and Engineering. Vol. 278, pp. 62-79. |
BibTeX:
@article{Keip2104,
author = {M.-A. Keip and P. Steinmann and J. Schröder},
title = {Two-scale computational homogenization of electroelasticity at finite strains},
journal = {Computer Methods in Applied Mechanics and Engineering},
year = {2014},
volume = {278},
pages = {62--79}
}
|
| Schrade, D., Müller, R., Gross, D. & Steinmann, P. (2014), "Phase field simulations of the poling behavior of BaTiO3 nano-scale thin films with SrRuO3 and Au electrodes", European Journal of Mechanics - A/Solids. Vol. 49, pp. 455-466. |
BibTeX:
@article{Schrade2014b,
author = {Schrade, D. and Müller, R. and Gross, D. and Steinmann, P.},
title = {Phase field simulations of the poling behavior of BaTiO3 nano-scale thin films with SrRuO3 and Au electrodes},
journal = {European Journal of Mechanics - A/Solids},
year = {2014},
volume = {49},
pages = {455-466},
note = {DOI: 10.1016/j.euromechsol.2014.08.007 P4 and P5}
}
|
| Endres, F. & Steinmann, P. (2014), "On an atomistic scale finite element method for the simulation of ferroelectric functional materials", Proceedings of the 2nd Seminar on The Mechanics of Multifunctional Materials. (12), pp. 17-20. |
BibTeX:
@article{Endres2014b,
author = {Endres, F. and Steinmann, P.},
title = {On an atomistic scale finite element method for the simulation of ferroelectric functional materials},
journal = {Proceedings of the 2nd Seminar on The Mechanics of Multifunctional Materials},
year = {2014},
number = {12},
pages = {17--20},
note = {P5}
}
|
| Endres, F. & Steinmann, P. (2015), "Molecular statics simulations of ferroelectric barium titanate in the rhombohedral phase", GAMM Mitteilung. Vol. 38(1), pp. 132-146. |
BibTeX:
@article{Endres2015,
author = {Endres, F. and Steinmann, P.},
title = {Molecular statics simulations of ferroelectric barium titanate in the rhombohedral phase},
journal = {GAMM Mitteilung},
year = {2015},
volume = {38},
number = {1},
pages = {132--146},
note = {P5}
}
|
Stand: 14.05.2015
Aktuelle Ergebnisse
In der ersten Projektphase wurde ein neuartiger molekularstatischer Algorithmus zur Simulation von Ferroelektrika entwickelt, implementiert und anhand elementarer Fragestellungen getestet. Dabei wurde eine Methode entwickelt, die die effiziente Bestimmung der makroskopischen Kontinuumsspannungen erlaubt und darüber hinaus auch die aus makroskopischen Spannungen resultierenden Verzerrungen berechnet. Mittels dieses Algorithmus war es erstmals möglich, nicht nur die dielektische Hysterese sondern auch die Schmetterling-Hysterese von Bariumtitanat auf atomarer Ebene zu simulieren. Neben der methodischen Entwicklung des Algorithmus wurden bereits verschiedene Domänenwandkonfigurationen von Bariumtitanat untersucht. Dabei konnten insbesondere größenabhängige Effekte von head to head und tail to tail Domänenwänden auf atomarer Ebene nachgewiesen werden. Des Weiteren wurde auch der Einfluss makroskopischer Spannungen auf 90° Nanodomänenwände analysiert. Unter anderem konnte dabei festgestellt werden, dass makroskopische Spannungen das Ausbilden der typischerweise laminaren 90° Domänenstrukturen gegenüber Monodomänen begünstigen. Somit tragen die bisher erzielten Ergebnisse zum allgemeinen, physikalischen Verständnis ferroelektrischer Materialien bei.
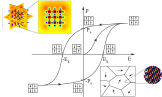
Die Simulation ferroelektrischer Materialien hat sich insbesondere im Bereich der teilchenbasierten Methoden in den letzten Jahrzenten weiterentwickelt. Diese Fortschritte sind zum einen auf der gestiegenen Rechenleistung moderner CPUs und zum anderen auf den Weiterentwicklungen der Simulationsmodelle zurückzuführen. Trotz all dieser Fortschritte ist die Lücke zwischen makroskopischen, meist auf Kontinuumsmechanik basierenden Ansätzen und Methoden auf atomistischen Längenskalen, wie beispielsweise der Molekulardynamik (MD), noch immer schwer zu überbrücken. Insbesondere die komplexen Energiepotentialformulierungen, welche langreichweitige Potentiale mit einschließen, erhöhen den Rechenaufwand für MD Berechnungen von Ferroelektrika enorm. Des Weiteren bewirken die für MD Simulationen benötigten Zeitschrittweiten einen zusätzlichen Rechenaufwand.

Um diese Nachteile der MD zu umgehen aber trotzdem Berechnungen mit atomistischer Auflösung zu ermöglichen wurde ein molekularstatischer Algorithmus basierend auf der finiten Elemente Methode (FEM) implementiert. Durch die drastische Verminderung des Berechnungsaufwands dieser Vorgehensweise ist es nicht nur möglich dielektrische Hysteresekurven von ferroelektrischen Kristallen zu berechnen, sondern auch mechanische Spannungen und Verzerrungen von Kristallen zu berücksichtigen. Dies ermöglicht nicht nur die Berechnung des piezoelektrischen Effekts sondern auch die Simulation des inversen piezoelektrischen Effekts auf atomarer Ebene. Dazu muss erwähnt werden, dass die meisten MD Algorithmen ein über die Zeit konstantes Volumen erfordern und somit zu Berechnungen komplexer Lastfälle nicht befähigt sind. Zwar gibt es Methoden, wie beispielsweise die Parrinello-Rahman Methode, um auch MD Simulationen Volumenänderungen in Folge mechanischer Spannungen zu ermöglichen, jedoch erhöhen diese den ohnehin enormen Rechenaufwand solcher Simulationen.
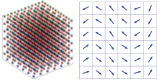
Der entwickelte Algorithmus bietet außerdem die Möglichkeit Phänomene wie Domänenwände und Randeffekte, wie sie beispielsweise bei Nanofilmen auftreten, zu untersuchen. Dabei dienen diese Berechnungen nicht nur der Vorhersage von Materialverhalten sondern tragen allgemein zum Verständnis für ferroelektrische Materialien bei. Zusätzlich tragen Analysen von Phänomenen, wie beispielsweise Domänenwänden, dazu bei, kontinuumsmechanische Modelle weiterzuentwickeln. Die meisten makroskopischen Ansätze können Domänenwände nur unzureichend auflösen. Somit kann beispielsweise die Berechnung von Energien und mechanischen Spannungen an Domänenwänden auf atomarer Ebene, zur Verbesserung kontinuumsmechanischer Modelle beitragen.




